What is convexity?

Convexity (γ) is a measure of the sensitivity and stability of duration over the yield curve, it describing the nonlinear price/yield relationship and accounts for the increasing slope of the price/yield curve and duration as the yield decreases, and vice versa.  Convexity is the first derivative of modified duration or the second derivative of price with respect to yield.  When convexity is high, the price/yield relationship will be curved and the reliability of the duration measurement will decrease for any change in prevailing interest rates.

Modified convexity (C_MOD) is the rate of change of modified duration (D_MOD) with respect to yield at the given starting yield, it measuring the curvature of the price function of an option-free instrument or a portfolio as yields change662bebcfadec5more than 100 bps, which modified duration cannot accurately measure.  It is calculated from convexity as follows, where r = periodic yield (i.e., nominal annual rate/compounding frequency per year):

C_MOD = Convexity/(1+r)²

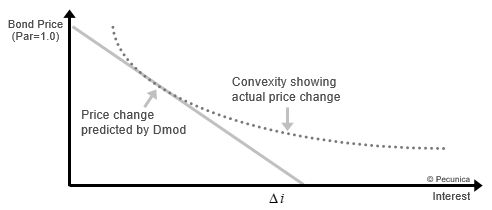
Option-free instruments display positive convexity.  Positive convexity is the slope of the price/yield showing that a rate-sensitive instrument’s price increases at an increasing rate when interest rates fall and decreases at a decreasing rate when rates rise.  Positive convexity causes the duration of the instrument to lengthen when rates fall and shorten when rates rise.  However, instruments that contain embedded options demonstrate negative convexity.

Modified Duration (Dmod) and Convexity

Source:

Instruments containing embedded options demonstrate negative convexity.  Negative convexity is the slope of the price/yield showing that a rate-sensitive instrument’s price increases at a decreasing rate when rates fall and decreases at an increasing rate when rates rise, it showing the limit to the change in price of a callable or puttable bond relative to an otherwise comparable straight bond.  Negative convexity causes the duration of an instrument to lengthen when rates rise and shorten when rates fall.

The effective convexity the convexity of a bond that takes into account the convexity of options embedded within the bond, it capturing the curvature of the observed price/yield relationship and may vary from the negative to the positive.  Depending on the amount of yield and the time to call, the price/yield relationship features positive convexity at high yields and negative convexity at low yields for immediately callable bonds.